Explain K-means Clustering Algorithm with examples.

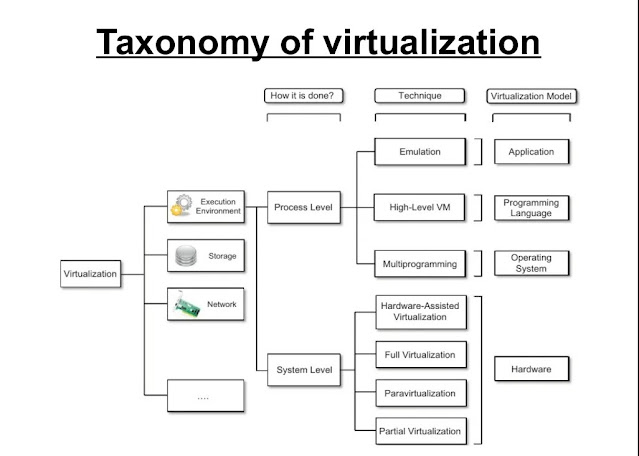
K-MEANS ALGORITHM

• K-Means Clustering is an Unsupervised Learning algorithm, which groups the unlabeled dataset into different clusters. Here K defines the number of pre-defined clusters that need to be created in the process, as if K-2, there will be two clusters, and for K-3, there will be three clusters, and so on.

•  K-means algorithm is a centroid-based clustering algorithm. The centroid of a cluster is its center point. For the k-means algorithm, the centroid is the mean of data points assigned to the cluster. Initially, it is a random value of the data point present in the given data set. 

• K-means algorithm takes dataset D and k as input and returns K-number of clusters. To find k- clusters first, it randomly selects k of the data points in D, each of which initially represents a cluster centroid. For each of the remaining data points, a data point is assigned to the cluster to which it is the most similar, based on the Euclidean distance between the data point and the cluster center. 

• The k-means algorithm then iteratively improves the within-cluster variation. For each cluster, it computes the new cluster center(mean) using the Data points assigned to the cluster in the previous iteration. All the data points are then reassigned using the updated means as the new cluster centers. The iterations continue until the assignment is stable, that is, the clusters formed in the current iteration are the same as those formed in the previous iteration.
• The k-means clustering algorithm mainly performs two tasks: 

- Determines the best value for K center points or centroids by an iterative process.

- Assigns each data point to its closest k-center. Those data points which are near to the particular k-center, create a cluster.

The below diagram explains the working of the K-means Clustering Algorithm: 

Advantages of K-means

• It is very simple to implement.
• It is scalable to a huge data set and also faster to large datasets.
• It adapts the new examples very frequently.
• Generalization of clusters for different shapes and sizes.

Disadvantages of K-means

• It is sensitive to the outliers.
• Choosing the k values manually is a tough job.

                                                          OR,

K-means Clustering Algorithm

k-means is one of the simplest unsupervised learning algorithms that solve the well-known clustering problem. The procedure follows a simple and easy way to classify a given data set through a certain number of clusters (assume k clusters) fixed apriori. The main idea is to define k centers, one for each cluster. These centers should be placed in a cunning way because different location causes the different result. So, the better choice is to place them as much as possible far away from each other.

Algorithmic steps for k-means clustering

Let X = {x1,x2,x3,........,xn} be the set of data points and V = {v1,v2,.......,vc} be the set of centers.

1) Randomly select ‘c’ cluster centers.

2) Calculate the distance between each data point and cluster center.

3) Assign the data point to the cluster center whose distance from the cluster center is the minimum of all the cluster centers.

4) Recalculate the new cluster center using:

, where, ‘ci’ represents the number of data points in i th cluster.

5) Recalculate the distance between each data point and newly obtained cluster centers.

6) If no data point was reassigned then stop, otherwise repeat from step 3.

Advantages

• Fast, robust, and easier to understand.
• Gives the best result when the data set is distinct or well separated from each other.

Disadvantages

• The learning algorithm requires apriori specification of the number of cluster centers.
• Randomly choosing the cluster center cannot lead us to a fruitful result.
• Applicable, only when mean, is defined i.e. fails for categorical data.
• The algorithm fails for the non-linear data set.

Thus after second iteration

Cluster 1= {p1,p2}

Cluster 2={p3,p4}

Now, new cluster centers are:

c1={(1+2)/2,(1+1)/2}={3/2,1} and c2={(2+4+5)/3,(1+3+4)/3}=(11/3,8/3)

Repeat this process till no re-assignment of points to groups.